Aubo机械臂位姿描述方式

修订日期	修订版本	修订内容	修订人
2022.09.29	V0.1	初始化文档	袁紫衣
2023.04.06	V0.2	补充问答 2	袁紫衣
2026.02.09	V0.3	补充修正描述内容	袁紫衣

1 Aubo示教器界面位姿描述

Aubo示教器界面采用 XYZ_RPY欧拉角来描述刚体位姿，其中位置(XYZ)没有什么难以理解的地方，姿态(RPY)的定义如下：

转动坐标轴的顺序为：X->Y->Z, 以固定坐标系的姿态作为参考(固定模式)，即先绕固定坐标系X轴旋转$\gamma$，再绕固定坐标系Y轴旋转$\beta$，再绕固定坐标系Z轴旋转$\alpha$，如下图所示。（需要注意与浮动模式的区别）
以右手法则为准，拇指指向为轴正方向，四指转向为角度正方向。

计算公式如下： $R(R_X,R_Y,R_Z) = Rot(z,\alpha)Rot(y,\beta)Rot(x,\gamma)$ 固定模式在数学表达式上表现为旋转矩阵左乘，浮动模式在数学表达式上表现为旋转矩阵右乘。两者的主要区别如下图所示：

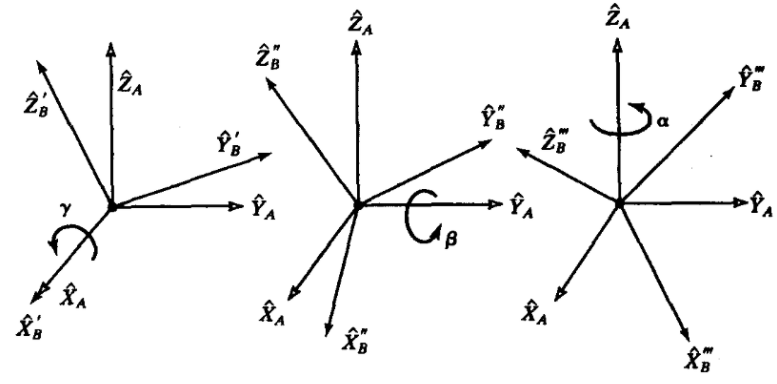
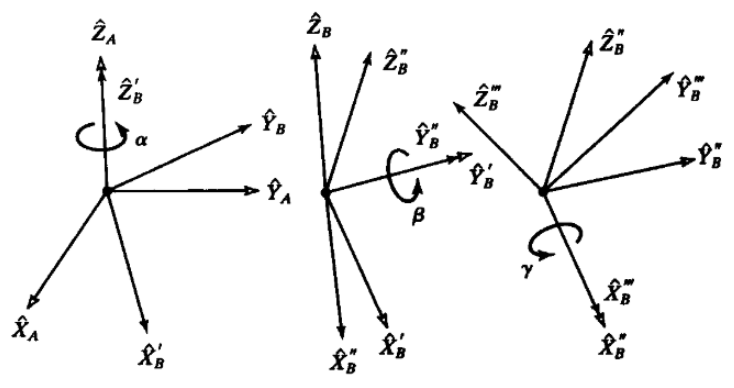
XYZ固定欧拉角（RPY） ZYX浮动欧拉角

要确定一个刚体在空间的位姿，须在物体上固连一个坐标系，然后描述该坐标系的原点位置和它三个轴的姿态，总共需要六个自由度或六条信息来完整地定义该物体的位姿。

理解欧拉角时，应该结合两个维度。1）旋转顺序（XYZ、ZYZ等); 2）参考坐标系（固定模式或者浮动模式）

2 欧拉角与四元数的相互转换

因为四元数在插值上存在诸多优势，机器人控制器在对姿态进行计算时，一般先转换成四元数来进行处理。

四元数根据实部和虚部的顺序不同，可以分成两种类型：

Hamilton顺序：$q=(q_w, q_x, q_y, q_z)$
JPL顺序：$q=(q_x, q_y, q_z, q_w)$

aubo控制器四元数采用Hamilton顺序。

绕坐标轴的多次旋转可以等效为绕某一转轴旋转一定的角度，四元数和欧拉角之间可以相互转化。

欧拉角转四元数

/**
 * @brief RPY欧拉角转四元数
 * @param rpy:欧拉角，绕固定坐标系XYZ转动，单位rad
 * @param ori:单位四元数，Hamilton顺序
 */
void Rpy2Quat(const double rpy[3], double ori[4])
{
    double roll, pitch, yaw, tmp;

    roll  = rpy[0] / 2.0;     //RX
    pitch = rpy[1] / 2.0;     //RY
    yaw   = rpy[2] / 2.0;     //RZ

    ori[0] = cos(roll) * cos(pitch) * cos(yaw) + sin(roll) * sin(pitch) * sin(yaw);
    ori[1] = sin(roll) * cos(pitch) * cos(yaw) - cos(roll) * sin(pitch) * sin(yaw);
    ori[2] = cos(roll) * sin(pitch) * cos(yaw) + sin(roll) * cos(pitch) * sin(yaw);
    ori[3] = cos(roll) * cos(pitch) * sin(yaw) - sin(roll) * sin(pitch) * cos(yaw);

    //严格归一化
    tmp = sqrt(ori[0] * ori[0] + ori[1] * ori[1] + ori[2] * ori[2] + ori[3] * ori[3]);
    ori[0] /= tmp;
    ori[1] /= tmp;
    ori[2] /= tmp;
    ori[3] /= tmp;
}

四元数转欧拉角

/**
 * @brief 四元数转RPY欧拉角
 * @param ori：单位四元数，Hamilton顺序
 * @param rpy：欧拉角，绕固定坐标系XYZ转动，单位rad
 */
void Quat2Rpy(const double ori[4], double rpy[3])
{
    //先转换成旋转矩阵
    double RotN[3][3];
    RotN[0][0] = 2 * (ori[0] * ori[0] + ori[1] * ori[1]) - 1;
    RotN[0][1] = 2 * (ori[1] * ori[2] - ori[0] * ori[3]);
    RotN[0][2] = 2 * (ori[1] * ori[3] + ori[0] * ori[2]);
    RotN[1][0] = 2 * (ori[1] * ori[2] + ori[0] * ori[3]);
    RotN[1][1] = 2 * (ori[0] * ori[0] + ori[2] * ori[2]) - 1;
    RotN[1][2] = 2 * (ori[2] * ori[3] - ori[0] * ori[1]);
    RotN[2][0] = 2 * (ori[1] * ori[3] - ori[0] * ori[2]);
    RotN[2][1] = 2 * (ori[2] * ori[3] + ori[0] * ori[1]);
    RotN[2][2] = 2 * (ori[0] * ori[0] + ori[3] * ori[3]) - 1;

    double eps = 1e-16;    //系统精度
    // old ZYX order (as per Paul book)
    if (fabs(RotN[0][0]) < eps && fabs(RotN[1][0]) < eps)
    {
        //singularity
        rpy[2] = 0.0;
        rpy[1] = atan2(-RotN[2][0], RotN[0][0]);
        rpy[0] = atan2(-RotN[1][2], RotN[1][1]);
    }
    else
    {
        rpy[2] = atan2(RotN[1][0], RotN[0][0]);
        rpy[1] = atan2(-RotN[2][0], sqrt(RotN[0][0] * RotN[0][0] + RotN[1][0] * RotN[1][0]));
        rpy[0] = atan2(RotN[2][1], RotN[2][2]);
    }
}

举例说明

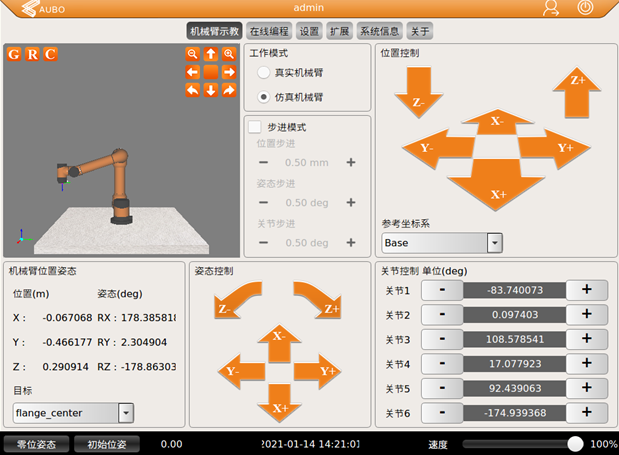
如上图所述，RPY 角分别为 RX = 178.3858， RY = 2.304904， RX = -178.86303：

基于上面规则，姿态变换顺序如下：

绕参考坐标系(Base)的 X 轴，旋转178.3858 度，得到姿态1;
姿态1绕参考坐标系(Base) Y 轴，旋转2.304904度，得到姿态2
姿态2绕参考坐标系(Base) Z 轴，旋转-178.86303 度，得到姿态3
姿态3就是目标相对于参考坐标系的姿态。

对应的四元数q 为：

q = [-0.01997, 0.0102021, -0.999647, -0.0142821]

注：q的符号在对姿态进行插值计算时需要进行转换，在静态描述某个姿态时，q与-q没有区别，表示同一个旋转。

3 常见问题解答

Question1

Question

为什么在机器人示教器中，当Rx、 Ry、 Rz的值不为0的时候，在全局模式下单独手动绕xyz中的一个轴旋转，但是RPY的值都变化？但是当Rx、 Ry、 Rz的值都为0的时候（目标坐标系与参考坐标系姿态相同），点击示教器上旋转姿态的任意一个按钮，点击的这个按钮对应的姿态坐标值变化，其他两个姿态坐标值不变？

Answer

因为 AUBO是采用固定的欧拉角描述方式，旋转矩阵相乘的顺序为 Z -> Y ->X，在全局模式下绕X或y轴旋转，相当于再左乘R(X)或R(Y)的旋转矩阵， Rx、 Ry、 Rz的角度都会变化，绕 z 轴旋转，相当于再左乘R(z)的旋转矩阵，只会改变 Rz 的角度。

Question2

Question

在设置工具坐标系后，绕工具坐标系 X 轴，Y轴或Z轴相对偏移一定角度时，其他姿态值为什么有变化？

Answer

因为 AUBO是采用固定的欧拉角描述方式，旋转矩阵相乘的顺序为 Z -> Y ->X，绕工具坐标系旋转时，相当于右乘旋转矩阵

绕工具坐标系 X 旋转，旋转矩阵相乘顺序为 Z -> Y ->X -> X，因此理论上只有 Rx 角度发生了变化，
绕工具坐标系 Y 旋转，旋转矩阵相乘顺序为 Z -> Y ->X -> Y，理论上 Rx、 Ry、 Rz的角度都会变化
绕工具坐标系 Z 旋转，旋转矩阵相乘顺序为 Z -> Y ->X -> Z，理论上 Rx、 Ry、 Rz的角度都会变化

由于工具坐标系的标定误差，以及姿态精度误差，由第三方测量仪检测时，理论上不会发生变化的值，实际上会有微小的变化。

4 相关参考

姿态描述方式参考2.3.机器人姿态描述简介
欧拉角的更多信息可以参考wikipedia: Euler_angles
四元数与三维旋转的关系可以参考这里

2.7.Aubo机械臂位姿描述方式